neutrales ElementDefinition neutrales Element
Schule
Universität
Es sei  eine Halbgruppe. eine Halbgruppe. 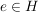 heißt linksneutrales (bzw. rechtsneutrales) Element von heißt linksneutrales (bzw. rechtsneutrales) Element von 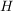 (bzgl. (bzgl.  ), wenn ), wenn
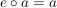 (bzw. (bzw.  ) )
für alle  gilt. gilt.
Ein zugleich links- und rechtsneutrales Element heißt neutral.
Beispiele
(1) In 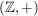 , ,  , , 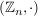 , ,  , ,  , , 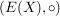 sind sind 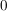 , , 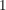 , , 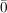 , ,  , , 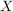 , ,  , ,  jeweils (in gleicher Reihenfolge) neutral. jeweils (in gleicher Reihenfolge) neutral.
(2) In
 , ,
versehen mit der Matrixmultiplikation, ist  linksneutral, aber nicht rechtsneutral. linksneutral, aber nicht rechtsneutral.
(3) Wenn man in einer beliebigen Menge 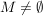 eine Verknüpfung eine Verknüpfung  durch durch  (für alle (für alle 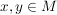 ) definiert, dann ist ) definiert, dann ist  eine Halbgruppe, in der jedes Element linksneutral ist. Hat eine Halbgruppe, in der jedes Element linksneutral ist. Hat 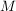 mehr als ein Element, dann gibt es in mehr als ein Element, dann gibt es in 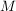 kein rechtsneutrales Element. kein rechtsneutrales Element.
Quelle: isbn3446130799
|