Wie man die Dimension eines Untervektorraumes berechnetGegeben: Vektorraum V über Körper K, Untervektorraum U
Gesucht:  (=Dimension des Vektorraums) (=Dimension des Vektorraums)
Die Berechnungsweise hängt natürlich davon ab, wie der Untervektorraum in der Aufgabenstellung gegeben ist; aus diesem Grund ist dieser Artikel danach gegliedert.
Dimensionsbestimmung eines Spanns gegebener Vektoren
Gegeben ist also eine (endliche) Menge von Vektoren  , die den Untervektorraum U aufspannen (ein Erzeugendensystem): , die den Untervektorraum U aufspannen (ein Erzeugendensystem):
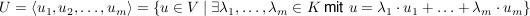
Für die Dimension gilt bei dieser Darstellung bereits: 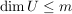 . .
Effiziente Berechnung
1. Schreibe die Vektoren  in die Zeilen (oder Spalten) einer Matrix. in die Zeilen (oder Spalten) einer Matrix.
2. Die Dimension des von  erzeugten Unterraumes erzeugten Unterraumes 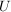 ist der Rang dieser Matrix. ist der Rang dieser Matrix.
Ist zusätzlich eine Basis des von  erzeugten Unterraumes erzeugten Unterraumes 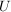 gesucht, so sollten die Vektoren gesucht, so sollten die Vektoren  in die Zeilen der Matrix geschrieben werden. Aus der Dreiecksgestalt der Matrix lassen sich sofort die Basisvektoren ablesen: Es sind dies die vom Nullvektor verschiedenen Zeilenvektoren der Dreiecksgestalt. Der Rang und damit die Dimension des Unterraums ist die Anzahl dieser Vektoren. in die Zeilen der Matrix geschrieben werden. Aus der Dreiecksgestalt der Matrix lassen sich sofort die Basisvektoren ablesen: Es sind dies die vom Nullvektor verschiedenen Zeilenvektoren der Dreiecksgestalt. Der Rang und damit die Dimension des Unterraums ist die Anzahl dieser Vektoren.
Umständliche Berechnung
Ein weiteres, aber umständliches Verfahren zur Dimensionsbestimmung ist nun, aus den gegebenen Vektoren eine Basis auszuwählen, also ein minimales Erzeugendensystem von 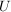 zu bestimmen. Die Anzahl der Basisvektoren ist dann die Dimension des Unterraums. zu bestimmen. Die Anzahl der Basisvektoren ist dann die Dimension des Unterraums.
Wir ermitteln schrittweise eine Basis, indem wir der Reihe nach die Vektoren  betrachten und uns jedes Mal fragen: betrachten und uns jedes Mal fragen:
Liegt der Vektor 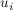 im Spann der bereits gefundenen Basisvektoren oder ist er mit den bisher gefundenen Basisvektoren linear unabhängig? im Spann der bereits gefundenen Basisvektoren oder ist er mit den bisher gefundenen Basisvektoren linear unabhängig?
Ist er linear abhängig, dann "überspringen" wir ihn, ist er linear unabhängig, wird er als weiterer Basisvektor genommen.
Formale Beschreibung:

 für für 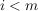
Die Entscheidung  kann in jedem Schritt durch Lösen eines linearen Gleichungssystems getroffen werden. kann in jedem Schritt durch Lösen eines linearen Gleichungssystems getroffen werden.
Für die auf diese Weise zuletzt gefundene Menge  gilt dann: gilt dann:  ist linear unabhängig und erzeugt den Unteraum ist linear unabhängig und erzeugt den Unteraum 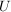 ( (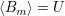 ). ).  bildet also eine Basis von bildet also eine Basis von 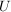 und die Anzahl der Vektoren in und die Anzahl der Vektoren in  ist die gesuchte Dimension von ist die gesuchte Dimension von 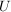 . .
Beispiele
 (siehe entsprechende (siehe entsprechende ![Link auf "https://matheraum.de/read?f=2&t=526&i=526" [link]](/images/popup.gif) Frage in unseren Foren) Frage in unseren Foren)

Es gilt: 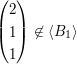 , also: , also: 
Es gilt (siehe Nebenrechnung 1 am Ende dieses Artikels):  und wir setzen und wir setzen 
Es gilt (siehe Nebenrechnung 2):  und wir setzen und wir setzen 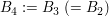
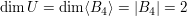
Nebenrechnung 1
Zu entscheiden ist: 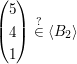
Diese Frage als lineares Gleichungssystem formuliert:

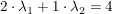

Addition des (-2)-fachen der ersten Zeile zur zweiten:
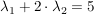


Einsetzen von 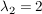 in die erste Gleichung: in die erste Gleichung:

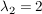

Einsetzen von  und und 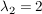 in die dritte Gleichung: in die dritte Gleichung:

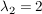
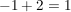 (wahr) (wahr)
Nebenrechnung 2
Zu entscheiden ist: 
Diese Frage als lineares Gleichungssystem formuliert:
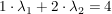
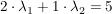
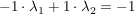
Addition des (-2)-fachen der ersten Zeile zur zweiten:


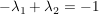
Einsetzen von 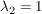 in die erste Gleichung: in die erste Gleichung:
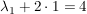
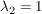
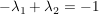
Einsetzen von  und und 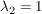 in die dritte Gleichung: in die dritte Gleichung:

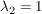
 (wahr) (wahr)
|