MatrixDefinition Matrix
In der linearen Algebra ist eine Matrix (Pl.: Matrizen) eine Anordnung von Zahlenwerten (aber auch anderen Objekten wie Operatoren) in Tabellenform.
Man spricht von den Spalten und Zeilen der Matrix, und bezeichnet selbige auch als Vektoren (d.h. Zeilenvektoren und Spaltenvektoren).
Die Objekte, die in der Matrix angeordnet sind, nennt man Komponenten oder Elemente der Matrix.
Wenn die Matrix m Zeilen und n Spalten besitzt, spricht man von einer m × n-Matrix (Merkregel: Zeilen zuerst, Spalten später), und nennt m und n die Dimensionen der Matrix.
Ist m = n spricht man von einer n × n oder quadratischen Matrix.
Die Komponente, die in der i-ten Zeile an j-ter Stelle steht, hat die Indices i,j. Eine allgemeine 2 × 3 Matrix A sieht zum Beispiel so aus:
Schule
Matrizen kann man zum Lösen von Linearen Gleichungssystemen als vereinfachende Schreibweise benutzen.
Matrizenkalkül
Bemerkung:
Das Produkt aus zwei Matrizen ist nur dann möglich, wenn sie "zusammenpassen".
Sie müssen also die richtigen Zeilen- und Spaltenanzahlen haben.
Hat die Matrix A n Spalten, dann muss die Matrix B genau n Zeilen haben.
Universität
Eigenschaften spezieller Matrizen
;bijektiv:
;idempotent: Eine Matrix 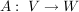 heißt idempotent, wenn die zugehörige lineare Abbildung idempotent ist bzw. wenn heißt idempotent, wenn die zugehörige lineare Abbildung idempotent ist bzw. wenn 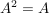 für alle für alle 
;injektiv:
;invertierbar:
;orthogonal:
;quadratisch:
;regulär:
;selbstadjungiert:
;selbstähnlich;
;surjektiv:
;symmetrisch:
;unitär:
siehe auch
charakterisches Polynom, Determinante, Koeffizientenmatrix, Rang
siehe auch: ![Link auf "http://de.wikipedia.org/wiki/Matrix_(Mathematik)" [link]](/images/popup.gif) http://de.wikipedia.org/wiki/Matrix_(Mathematik) http://de.wikipedia.org/wiki/Matrix_(Mathematik)
|