QuotientenkriteriumSatz Quotientenkriterium
Universität
Voraussetzungen und Behauptung
Bemerkungen.
Beispiele.
Nun ein paar Beispiele zum Quotientenkriterium:
1) Gegeben sei die Reihe 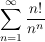
Wir wollen also nachweisen, dass dieses Reihe absolut konvergiert.
Lösung:
Existiert ein 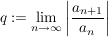
dann konvergiert die Reihe
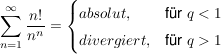
Nun wird eingesetzt und ein wenig gerechnet:
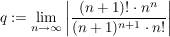
ich habe also den Doppelbruch vereinfacht.

Bemerkung:
Es gilt: 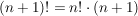
Nun kann man ein wenig kürzen und erhält:
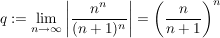
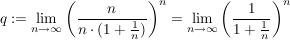
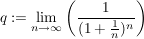
Nun weiß man aus der Vorlesung das folgendes gilt:
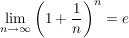

Wir haben also 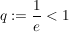
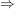 Die Reihe Die Reihe 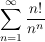 ist absolut konvergent ist absolut konvergent
Ich werde nach und nach weitere Beispiele hinzufügen.
Beweis.
|