NullstellenbestimmungGegeben sei eine ganzrationale Funktion der Form 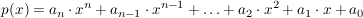 . .
Gesucht sind die Nullstellen, also die Werte für x, so dass p(x)=0 gilt.
Leider gibt es nur für bestimmte ganzrationale Funktionen explizite Lösungsverfahren für das Nullstellenproblem; diese werden im Folgenden vorgestellt.
Konstante Funktionen (Grad 0; 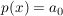 ) )
haben entweder keine Nullstelle (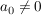 ) )
oder sind überall Null (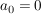 ) )
Lineare Funktionen (Grad 1; 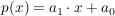 ) )
haben max. eine Nullstelle.
Wenn sie die Steigung 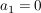 haben und nicht durch den Ursprung verlaufen, haben sie keine Nullstelle. haben und nicht durch den Ursprung verlaufen, haben sie keine Nullstelle.
Quadratische Funktionen (Grad 2; 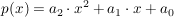 ) )
Die Lösung(en) einer quadratischen Gleichung der Form:
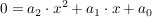
lauten (sofern die Ausdrücke definiert sind)
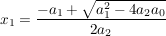
und
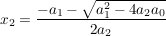 . .
In Kurzschreibweise:
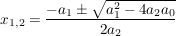 . .
Die Lösung(en) einer quadratrischen Gleichung der Form
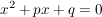 lauten (sofern die folgenden Ausdrücke definiert sind): lauten (sofern die folgenden Ausdrücke definiert sind):

und
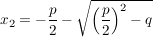 . .
In Kurzschreibweise:
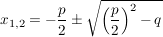 . .
Quadratische Ergänzung
Eine Quadratische Ergänzung nennt man die Erweiterung eines Terms der Form
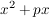
zu einer binomischen Formel:

Gegeben sei eine quadratische Funktion 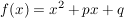
Gesucht seien die Nullstellen 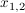
Dann gilt:
mit 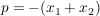 und und 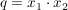
Effektivere Behandlung von Spezialfällen
Ganzrationale Funktionen höheren Grades (Grad 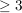 ) )
siehe auch:
kubische Gleichung
![Link auf "http://www.mathematik.ch/anwendungenmath/Cardano/FormelCardano.php" [link]](/images/popup.gif) Cardano-Formel Cardano-Formel
![Link auf "http://www.fh-lueneburg.de/mathe-lehramt/mathe-lehramt.htm?show=http://www.fh-lueneburg.de/mathe-lehramt/algebra/gleichung/cardano.htm" [link]](/images/popup.gif) FH Lüneburg FH Lüneburg
Horner-Schema
Numerische Verfahren
|