MiniMaxAufgabenVerfahren bei Extremwertaufgaben
Schule
Aufgabe:
Gegeben ist ein Zaun mit einer Länge von 20 m.
Mit ihm soll eine möglichst große Fläche umschlossen werden, die an einer Seite von einer Hauswand begrenzt wird.
Vorüberlegung:
Gesucht ist: A = a * b , also die Fläche, die maximal werden soll (Extremalbedingung EB).
Gegeben ist der Umfang der Fläche U = 2a + b (Nebenbedingung NB).
Eliminierung einer Variablen:
Da wir Funktionen mit mehr als einer Variablen (in der Schule) nicht untersuchen können, müssen wir eine Variable mit Hilfe der NB ersetzen: b = U - 2a (*)
einsetzen in EB:
das ist nun eine Funktion, die nur noch von a abhängt.
Extremwert-Untersuchung:
Deren Maximum kann man mit der Differentialrechnung bestimmen:
Wegen A"(a) = - 4 < 0 liegt an der Stelle  ein Maximum vor. ein Maximum vor.
Die maximale Fläche ergibt sich durch
Aus der Gleichung (*) ergibt sich die Begrenzung für a: 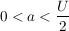 . .
Kontrolle der Randextrema:
An den "Rändern" könnte zufällig ein größerer Wert als das relativie Extremum herauskommen:
A(0) = 0 und 
(Da A(a) eine quadratische Funktion ist, hätte man sich das auch aus dem bekannten Verlauf solcher Funktionen herleiten können.)
Übungsaufgaben
|