www.vorhilfe.de
- Förderverein -
Der Förderverein.

Gemeinnütziger Verein zur Finanzierung des Projekts Vorhilfe.de.
Hallo Gast! [ einloggen | registrieren ]
Startseite · Mitglieder · Impressum
Forenbaum
^ Forenbaum
Status VH e.V.
  Status Vereinsforum

Gezeigt werden alle Foren bis zur Tiefe 2

Navigation
 Startseite...
 Suchen
 Impressum
Das Projekt
Server und Internetanbindung werden durch Spenden finanziert.
Organisiert wird das Projekt von unserem Koordinatorenteam.
Hunderte Mitglieder helfen ehrenamtlich in unseren moderierten Foren.
Anbieter der Seite ist der gemeinnützige Verein "Vorhilfe.de e.V.".
Partnerseiten
Weitere Fächer:

Open Source FunktionenplotterFunkyPlot: Kostenloser und quelloffener Funktionenplotter für Linux und andere Betriebssysteme
Größen
Mach mit! und verbessere/erweitere diesen Artikel!
Artikel • Seite bearbeiten • Versionen/Autoren

Größen

Der Begriff: Größe

Eine Größe kann von qualitativer oder auch quantitativer Art sein.

In den Naturwissenschaften wird eine (quantitative) Größe auch physikalische Größe genannt. Sie besteht aus Zahlenwert (auch Maßzahl) und Einheit.

z.B.:  Die Länge einer bestimmten Strecke beträgt s=128m. Hier 128 ist der Zahlenwert, m ist die Einheit für das Meter - beides wird formal miteinander multipliziert s=128*m

Es kann vorkommen, dass die Darstellung einer physikalischen Größe mit der verwendeten Einheit unvorteilhaft ist. Beispielsweise könnte die Einheit eine sehr große oder sehr kleine Zahl zur Beschreibung eines physikalischen Vorganges erfordern. Hier behilft man sich mit sogenannten Vorsatzzeichen:

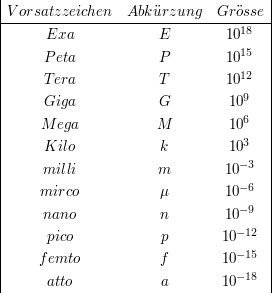
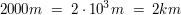
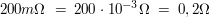
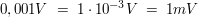
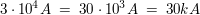
$ \begin{array}{|\ c\ |\ c\ |\ c\ |} Vorsatzzeichen & Abk"urzung & Gr"osse\\ \hline Exa & E & 10^{18}\\ Peta & P & 10^{15}\\ Tera & T & 10^{12}\\ Giga & G & 10^{9}\\ Mega & M & 10^6\\ Kilo & k & 10^3\\ milli & m & 10^{-3}\\ mirco & \mu & 10^{-6}\\ nano & n & 10^{-9}\\ pico & p & 10^{-12}\\ femto & f & 10^{-15}\\ atto & a & 10^{-18}\\ \end{array} $

Beispiele


$ 2000m\ =\ 2\cdot{}10^{3}m\ =\ 2km $

$ 200m\Omega\ =\ 200\cdot{}10^{-3}\Omega\ =\ 0,2\Omega $

$ 0,001V\ =\ 1\cdot{}10^{-3}V\ =\ 1mV $

$ 3\cdot{}10^4A\ =\ 30\cdot{}10^{3}A\ =\ 30kA $



Übersicht von Größen aus der Regelungstechnik




Erstellt: Fr 01.12.2006 von Herby
Letzte Änderung: Mi 04.11.2009 um 09:53 von Herby
Weitere Autoren: Loddar
Artikel • Seite bearbeiten • Versionen/Autoren • Titel ändern • Artikel löschen • Quelltext
^ Seitenanfang ^
ev.vorhilfe.de
[ Startseite | Mitglieder | Impressum ]