EigenvektorEigenvektoren
Definition
Sei 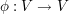 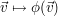 ein Endomorphismus und A die dazugehörige (eindeutig) Darstellungsmatrix. ein Endomorphismus und A die dazugehörige (eindeutig) Darstellungsmatrix.
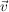 ist genau dann ein Eigenvektor von ist genau dann ein Eigenvektor von 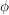 , wenn , wenn 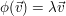 gilt. Es muss weiterhin gelten gilt. Es muss weiterhin gelten 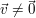 , d.h. der Nullvektor ist per definitionem kein Eigenvektor. (0 darf aber dagegen ein Eigenwert sein). , d.h. der Nullvektor ist per definitionem kein Eigenvektor. (0 darf aber dagegen ein Eigenwert sein).
Berechnung von Eigenvektoren
Um Eigenvektoren zu berechnen, berechnet man zunächst die Eigenwerte der Matrix, also die Nullstellen des Charakteristischen Polynoms.
Als nächstes berechnet man dann die Eigenräume zum Eigenwert 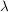 . .
Alle Vektoren, die dann im Eigenraum zum dazugehörigen Eigenwert 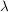 liegen, sind Eigenvektoren. liegen, sind Eigenvektoren.
Theorie
Die Dimension des Eigenraumes ist höchstens so groß, wie die Multiplizität des Eigenwertes. Die Dimension des Eigenraumes nennt man auch Geometrische Vielfachheit und die Multiplizität des Eigenwertes auch Algebraische Vielfachheit. Es gilt also:
geom. Vielfachheit 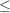 algebraische Vielfachheit algebraische Vielfachheit
Beispiel
Es sei ein Endomorphismus durch die darstellende Matrix 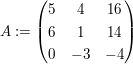
1) Berechnen des charakteristischen Polynoms
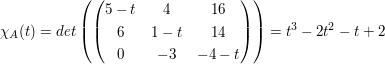
2) Berechnen der Nullstellen des char. Polynoms, also der Eigenwerte
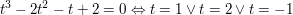
3) Berechnen der Eigenräume zu den entsprechenden Eigenwerten:
3.1) Eigenraum zum Eigenwert t=1:
Hinweis: Mit N ist der Nullraum der Matrix gemeint. Der Nullraum ist das selbe wie der Kern einer Matrix.
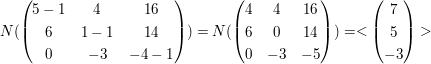
Bei der Bestimmung des Nullraumes ergibt sich eine Nullzeile. Das muss auch so sein, denn man hat den Eigenwert ja genau so bestimmt, dass die Determinante von A-t*1 genau Null wird, also dass die Matrix nicht invertierbar ist.
3.2) Eigenraum zum Eigenwert t=2:
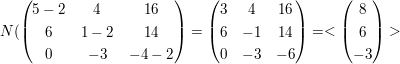
3.3) Eigenraum zum Eigenwert t=-1:
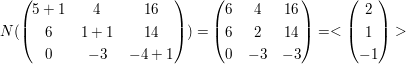
|