Benutzer:tobit09/Beweis-Tutorial A7Beweis-Tutorial
 3. "es existiert"-Aussagen 3. "es existiert"-Aussagen
Lösungsvorschlag Aufgabe 7
Aufgabe:
Seien  reelle Zahlen mit reelle Zahlen mit 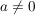 . Zeige, dass eine reelle Zahl . Zeige, dass eine reelle Zahl  existiert mit existiert mit  . .
Überlegungen zur Lösung:
Beispielsweise mit Schmierzettel-Methode ein Beispiel für  finden: finden:
1. Wenn  gilt, muss gilt, muss  und somit wegen und somit wegen 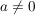 die Gleichung die Gleichung  erfüllt sein. erfüllt sein.
2. Tatsächlich gilt beispielsweise für  (ergibt Sinn, da (ergibt Sinn, da 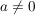 ) wie gewünscht ) wie gewünscht  . .
Lösungsvorschlag:
Für die reelle Zahl  (ergibt Sinn, da (ergibt Sinn, da 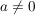 ) gilt ) gilt  . Insbesondere existiert eine reelle Zahl . Insbesondere existiert eine reelle Zahl  mit mit  . .
|