Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
| argl, Tyskie84 | www.matheraum.de
Oberstufenmathematik - Analysis/Analytische Geometrie
Aufgabenblatt 5
Abgabe: Do 29.01.2009 19:00 | 30.12.2008 | | | | Aufgabe 1 |
Gegeben seien die Funktionen  und und 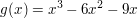 . .
a) Untersuchen Sie f auf Nullstellen, Extrema und Wendepunkte. Bestimmen Sie jeweils die Koordinaten der Punkte und geben Sie diese an.
b) Erstellen Sie eine Wertetabelle für 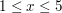 . .
c) Zeichnen Sie die Graphen von f und g für 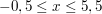 in ein gemeinsames Koordinatensystem. in ein gemeinsames Koordinatensystem.
d) Zeigen Sie, dass f und g genau zwei Punkte gemeinsam haben.
e) Zeigen sie, dass die Graphen von f und g sich in gleichgrossen Winkeln schneiden und bestimmen Sie die grösse dieser Schnittwinkel.
f) Bestimmen Sie den Flächeninhalt der von f und g eingeschlossenen Fläche.
g) Zeigen Sie, dass die Wendetangenten von f und g parallel verlaufen. Die Wendetangenten bilden mit den Koordinatenachsen ein Trapez. Bestimmen Sie dessen Flächeninhalt.
h) Die Graphen von f und g schneiden aus den Parallelen zur y-Achse für  eine Strecke heraus. Bestimmen Sie die maximale Länge dieser Strecken. eine Strecke heraus. Bestimmen Sie die maximale Länge dieser Strecken. | | Aufgabe 2 |
Gegeben seien die Funktionen 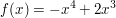 und und 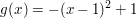
a) Bestimmen Sie Nullstellen, Extrema und Wendepunkte von f.
b) Zeichnen Sie die Graphen von f und g im Intervall 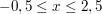 in ein gemeinsames Koordinatensystem. in ein gemeinsames Koordinatensystem.
c) Bestimmen Sie die Schnittpunkte von f und g im betrachteten Intervall.
d) Bestimmen Sie die Grösse der Schnittwinkel für die ermittelten Schnittpunkte.
e) Bestimmen Sie den Inhalt der von f und g im ersten Qudranten eingeschlossenen Fläche.
f) Ein achsenparalleles Rechteck mit einer Ecke im Ursprung und der gegenüberliegenden auf dem Graphen von f soll maximalen Inhalt haben. Bestimmen Sie den entsprechenden x-Wert.
g) Für welches a (0 < a < 2) ist der Inhalt zwischen dem Graphen von g und der x-Achse gleich 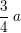 ? ?
|
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|