Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
| Lineare Algebra I/II,
Vorkurs, | www.matheraum.de
Lineare Algebra
Aufgabenblatt 1
Abgabe: Mo 06.02.2012 10:00 | 30.01.2012 | | Die Übungsaufgaben beziehen sich auf das Buch "Lineare Algebra" von Gerd Fischer bzw. auf das Inhaltsverzeichnis, das in der Kursbeschreibung zu finden ist. Die Übungsaufgaben (i.d.R. zu immer einem neuen Kapitel im Buch) können bequem in einer Woche gelöst werden. | | Für die erste Aufgabenserie liegt das Kapitel über "Mengen, Abbildungen, Relationen" zu Grunde. Vertraute Begrifflichkeiten sollten sein: Menge, Teilmenge, Leere Menge, Vereinigung, Durchschnitt, Indexmenge, Differenzmenge(Komplement), Abbildung, Bild, Urbild, injektiv, surjektiv, bijektiv, Umkehrabbildung, Komposition, Identität, direktes Produkt, Graph, Relation & Eigenschaften, Äquivalenzrelation, Äquivalenzklasse. | | Aufgabe 1 | Aufgabe I-1: Seien M = {1;3} und N = {1;2;5}. Entscheiden Sie, ob folgende Aussagen richtig oder falsch sind. Begründen Sie Ihre Antworten!
(a) M  N N
(b) M 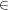 N N
(c) 1  M M
(d) M und N sind disjunkt
(e) 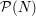 und und 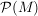 sind disjunkt. sind disjunkt. 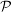 bezeichne hierbei die Potenzmenge. bezeichne hierbei die Potenzmenge. | | Aufgabe 2 | Aufgabe I-2: Beweisen Sie die folgenden Rechenregeln für die Operationen mit Mengen:
(a) X 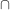 Y = Y Y = Y 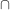 X X
(b) X 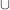 (Y (Y 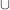 Z) = (X Z) = (X 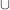 Y) Y) 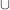 Z , Z ,
(c) X \ (Y 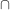 Z) = (X \ Y) Z) = (X \ Y) 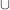 (X \ Z) (X \ Z) | | Aufgabe 3 | Aufgabe I-3: Untersuchen Sie die folgenden Abbildungen auf Injektivität, Surjektivität und Bijektivität:
(a) f: 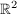 -> -> 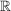 ; (x,y) ; (x,y)  x + y x + y
(b) g: 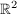 -> -> 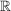 ; (x,y) ; (x,y) 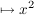 + + 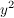 - 1 - 1
Zeigen Sie außerdem für zwei Abbildungen 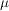 : X -> Y , : X -> Y ,  : Y -> Z : : Y -> Z :
(c) Sind 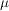 und und  injektiv (surjektiv), so ist auch die Hintereinanderausführung injektiv (surjektiv), so ist auch die Hintereinanderausführung 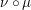 : X -> Z injektiv (surjektiv). : X -> Z injektiv (surjektiv). | | Aufgabe 4 | Aufgabe I-4: Untersuchen Sie die folgenden Relationen ~ auf der Menge M auf Reflexivität, Symmetrie, Transitivität, Antisymmetrie und Vollständigkeit. Handelt es sich um eine Äquivalenzrelation?
(a) M: Menge aller Dreiecke in einer geg. Ebene; Es sei a~b genau dann, wenn a ähnlich zu b
(Zusatz) 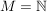 ; es sei a~b genau dann, wenn a die Zahl b ohne Rest teilt ; es sei a~b genau dann, wenn a die Zahl b ohne Rest teilt |
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|