Vorhilfe - Kostenlose Kommunikationsplattform für gegenseitige Hilfestellungen
URL: http://verein.vorhilfe.de/vorkurszettel?id=79
| argl, Tyskie84 | www.matheraum.de Oberstufenmathematik - Analysis/Analytische Geometrie Aufgabenblatt 6 Abgabe: Mo 30.03.2009 07:00 | 28.02.2009 |
| Aufgabe 1 | ||
| Berechne:
a) 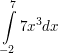 b) 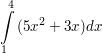 c) 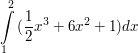 d) 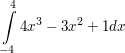 e)  f) 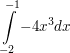 h)  | ||
| Aufgabe 2 | ||
| Vereichfache erst, berechne dann!
a)  b)  c)  d)  | ||
| Aufgabe 3 | ||
| Berechne:
a) 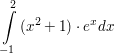 b) 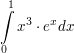 c)  d) 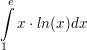 Berechne das Integral und gib eine Stammfunktion zum Integranden an: a)  b) 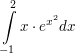 c) 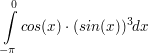 d) 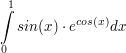 e)  f) 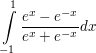 Berechne eine Stammfunktion zu f: a) b) c) d) | ||
| Aufgabe 4 | ||
| Gegeben ist die Funktion | ||
© Copyright 2003-25 ev.vorhilfe.de
Der Inhalt dieser Seite kann -- sofern nicht anders lautend gekennzeichnet -- durch jedermann gemäß den Bestimmungen der Lizenz für Freie Inhalte genutzt werden.
Der Inhalt dieser Seite kann -- sofern nicht anders lautend gekennzeichnet -- durch jedermann gemäß den Bestimmungen der Lizenz für Freie Inhalte genutzt werden.